Absolute measurement of absorption and scattering coefficients spectra of a multiply scattering medium

Sergio Fantini *, Maria Angela Franceschini *, Joshua B. Fishkin, and Enrico Gratton
Laboratory for Fluorescence Dynamics, Department of Physics, University of Illinois at Urbana- Champaign, 1110 West Green Street, Urbana, Illinois 61801-3080
 
 

* Permanent Address:Istituto di Elettronica Quantistica-Consiglio Nazionale delle Ricerche, via Panciatichi 56/30, 50127 Firenze, Italy
 
 

ABSTRACT
On the basis of the diffusion theory model, frequency-domain spectroscopy allows for a quantitative determination of the absorption (ua) and scattering (us') coefficient spectra of a homogeneous multiply scattering medium. We performed measurements using an intensity modulated light emitting diode (LED) as the light source. The LED's spectral distribution permits the study of a spectral region extending for about 80 nm. Data sets (phase shift and average intensity) at two different source-detector distances are acquired: the absorption and scattering coefficient spectra of the medium are then calculated from analytical expressions for ua and us'. Methylene blue (peak absorption wavelength 656 nm) is used as a test absorbing material. The methylene blue is dissolved in an aqueous Liposyn solution which serves as the multiply scattering medium. The relative amounts of absorber and scatterer are chosen such that the values of ma and ms' match typical values in tissues. The results obtained for ua(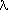) with this LED based technique are in quantitative agreement with those obtained with a standard spectrophotometer in a non- scattering regime.

1. INTRODUCTION
The determination of the optical properties of tissues is important in many fields of medicine, both for tissue diagnostics and the monitoring of physiologically important processes [1-5]. In particular, the measurement of the concentration of a chromophore in biological tissues can provide useful information. A spectroscopic study of tissues is complicated by the fact that they are multiply scattering media, and thus the attenuation of light is due both to absorption and scattering. The problem of separating the effects of absorption and scattering has been treated using steady state [6-8], and time resolved techniques (in both the time-domain [9] and frequency-domain [10,11]). We have performed measurements in the frequency-domain, in which the intensity of the light source is modulated at radio frequency (typically at tens to hundreds of megahertz), and the detected quantities are the average intensity (DC component), the amplitude of the intensity oscillation (AC component), and the phase shift of the detected light relative to the exciting signal (Ph). A model based on the diffusion approximation to the Boltzmann transport equation has been developed [12]. It provides expressions for the measured quantities (DC,AC,Ph) in terms of the optical parameters of the medium, which are the absorption coefficient (ua), the transport scattering coefficient (us') and the index of refraction (n). This model is valid for a homogeneous medium in a multiply scattering regime and far from sources or boundaries. We used a light emitting diode (LED) as the light source, and we developed an experimental protocol, based on a two-distances measurement, which allows for the determination of ua and us' from analytical expressions. The measurable ranges of ua and us', as well as the sensitivity of this method to changes in ua and us', are discussed.

2. METHODS
The medium we have studied is an aqueous solution of Liposyn III 20% (an intravenous fat emulsion) from Abbott Laboratories, in which a test absorbing material (methylene blue) was dissolved. The concentration of Liposyn, which provided the scattering material, was chosen to be 7.7% by volume (i.e. solids content of 1.54%) yielding a medium scattering coefficient on the order of 20 (1/cm), which is typical for soft tissues [13]. Methylene blue has an absorption spectrum peaked at 656 nm and an extinction coefficient of 182 (1/(cm*mM)) at 664 nm [14]. We used several concentrations of methylene blue, from 0 to 0.450 uM, in order to cover a typical range of values of ua in tissues (0.01 to 0.1 1/cm) [13]. The measurements were conducted in a 2.3 l cylindrical container whose dimensions were 9 cm in height and 18 cm in diameter.

 As the light source, we utilized a light emitting diode (LED) manufactured by Hewlett Packard (part number: HLMP-4101). We modulated the LED's intensity by applying a sinusoidal voltage generated by a frequency synthesizer (Marconi Instruments, Model 2022A) and amplified by an ENI Model 403 LA RF Amplifier. In general, a frequency domain measurement is more accurate at higher modulation frequencies, so we looked for the highest frequency of the sinusoidal voltage supply which provided a good AC signal at the LED's output. This frequency was 60 MHz for the LED we used, and the peak to peak supplied voltage was 10 V. The negative front of the sinusoidal voltage was less than the reverse breakdown voltage of the LED (15 V). In these working conditions the LED's output was characterized by a peak wavelength of 665 nm, a spectral line fullwidth at half maximum of about 30 nm, a total power of about 0.2 mW, and a modulation ratio (AC/DC) of 60%. Its spectral emission enabled us to accomplish measurements at wavelengths ranging from 620 to 700 nm, which is appropriate for measuring the spectrum of methylene blue (lmax = 656 nm).

 The multiply scattered light was detected by a bundle of glass optical fibers of overall diameter of 3 mm. This bundle was positioned at a distance r from the light source, and its output was dispersed via a monochromator (10 cm ISA Instrument SA, Inc.) and detected by the sample photomultiplier tube (PMTs). The spectral resolution was 4 nm. The detection system is a typical one for frequency domain measurements, and is based on a well established cross-correlation technique [15,16]. The cross-correlation frequency was set to 80 Hz. We referenced the values of DC, AC and phase detected by the sample PMT (PMTs) to those detected by the reference PMT (PMTr) which collected a signal from an optical fiber in close contact with the LED (both PMT's are manufactured by Hamamtsu (Japan), model R928). This procedure provided a correction for variations in the LED's output characteristics that might have occured during the measurement. The experimental setup is shown in Fig. 1 .

 Fig. 1. Experimental setup.
 
 

The diffusion approximation to the Boltzmann transport equation provides analytical expressions for the frequency-domain parameters as a function of the absorption coefficient (ua), the transport scattering coefficient (us'), and the index of refraction (n) of the medium [12]. These expressions, which are valid for a homogeneous infinite medium at points which are far from sources and boundaries, predict a linear dependence of Ph, ln(rUdc) and ln(rUac) on r (where r is the source-detector separation, Udc is the DC component of the photon density, Uac is the amplitude of the AC component of the photon density). If we consider two different source detector separations, let's say r1 and r2 with r1< r2, we can define the following quantities:
 
 

.
 
 

Finally, making the further assumption that w/2p< < cus'/n (where w/2p is the modulation frequency, and c is the speed of light in vacuum) we can write [12]:
 
 

(1)
 
 

(2)
 
 

(3)
 
 

We observe that the condition w/2p< < cus'/n holds for most biological tissues in the red-near IR spectral region for modulation frequencies up to 1 GHz. The idea is then to perform two measurements at two different source-detector separations (r1 and r2) from which to obtain dc, ac, ph. We point out that the source terms do not appear in Eqs. 1-3, so that dc, ac, ph depend only on the modulation frequency and on the optical parameters of the medium. Furthermore, the spectral instrument response factor cancels in dc and ac because they contain the ratio of Udc and Uac measured at different source-detector separations, but at the same wavelength. Once dc, ac, ph are measured ua and us' can be calculated from Eqs. 1-3. Inspection of these equations shows that they are not independent since they contain only two unknowns, i.e. ua/n and n(ua+us'). If n is known, one can choose to obtain ua and us' from three different sets of measurements: dc and ph (DC and phase), ac and ph (AC and phase), dc and ac (DC and AC). The analytical expressions for ua and us' in the three cases are given in Table 1.
 
 

On the basis of these expressions, the errors on ua and us' can be evaluated from the estimates of the errors on dc, ac, ph. The result is that, for typical values of the parameters in tissues, the errors on ua and us' in the (dc,ac) measurement scheme are much larger than those in the (dc,ph) and (ac,ph) schemes. This is due to the fact that the values of dc and ac are very close, differing by no more than a few percent. We chose to use the (dc,ph) scheme because the error on the DC signal is typically smaller than the error on the AC signal. The use of DC and phase in frequency-domain measurements was also suggested as an alternative to a phase and modulation (AC/DC) measurement [10]

 In summary, our measurement protocol consists of acquiring data at two source-detector distances (r1, r2) and calculatedc and ph. From the expressions relative to the (dc,ph) measurement scheme in Table 1, we obtain the values of ua and us'. This procedure, applied wavelength by wavelength within the whole spectral region covered by the LED (620 to 700 nm) provides the spectra of ua and us'. The choice of the values of r1 and r2 (r1< r2) relies on two considerations:
 
 

We chose r1 to be 1.5 cm, while r2 ranged from 4.0 to 2.5 cm depending on the amount of absorber in the medium.

3. RESULTS
First we performed a control measurement on the aqueous Liposyn solution alone. In the absence of methylene blue we expect to measure essentially the absorption spectrum of water, while the scattering spectrum is related to the suspended particles of Liposyn. In Fig. 2 we show the spectra we measured for ua and us'. The spectrum of ua is compared to values of ua for water measured at several wavelengths by Hale and Querry [17]. The order of magnitude of ua is the same for both quantities and their spectral dependence is qualitatively comparable. We attribute the deviations from the literature values of ua for water to a contribution of the Liposyn to absorption, and to boundary effects due to the finite size of the container we used. The spectrum of us' is compared to the curve us'(l) predicted by van Staveren et al. on the basis of Mie theory calculations for 1.54% Intralipid [18]. Even if van Staveren considered a slightly different medium, we observe that the values of us' and the spectral dependence are essentially reproduced.

 Fig. 2. Scattering (solid line) and absorption (dashed line) coefficients spectra of the Liposyn solution containing no methylene blue. The two spectra are compared respectively with us'(l) predicted by van Staveren et al. (dotted line), and with several values of ua(l) for water known in literature (symbols).

 Next we measured the absorption spectra for different concentrations of methylene blue in the Liposyn solution. We subtracted the absorption spectrum of the Liposyn solution containing no methylene blue to obtain the corrected absorption spectra for methylene blue alone. The results obtained with our measurement protocol were then compared to the absorption spectra obtained with a spectrophotometer (Perkin Elmer LAMBDA 5) for the same concentrations of methylene blue in a non scattering solution. The comparison, reported in Fig. 3 for three methylene blue concentrations, shows a quantitative agreement between the measurements in the multiply scattering regime (performed via the frequency-domain LED technique) and the measurements in minimal scattering regime (performed by a standard spectrophotometer). We have also analyzed the dependence of ua and us' on methylene blue concentration. The result is shown in Fig. 4 for l=680 nm: us' is essentially unaffected by the concentration of absorber, while ua shows a linear dependence. We observe that our results have been obtained by assuming that n=1.33 (which is the index of refraction of water in the spectral region considered). The good quantitative results we found justify such a choice for n.

 Fig. 3. Quantitative comparison between methylene blue absorption coefficient spectra measured in the strongly scattering medium by the LED technique (symbols) and in a non-scattering regime by a spectrophotometer (lines). The spectra correspond to MB concentrations of 0.090, 0.225, and 0.450 uM as labeled. Errors bars for the experimental data relative to the strongly scattering medium are shown every 20 nm.

 Fig. 4. Dependence of the values of ua and us' at 680 nm on methylene blue concentration. The straight lines are obtained by a weighted least square method. When the error bars are not displayed they are on the order of the symbol dimensions.
 
 

4. DISCUSSION
The range of values for ua and us' that can be measured with the frequency-domain LED method is determined by the following conditions:
 
  By imposing these conditions we can evaluate the ranges of measurable values of ua and us' using our instrument. The result is shown on a us'-ua log-log diagram in Fig. 5 , where one can see that the typical values of ua and us' in tissues fall inside the measurable region of the us'-ua plane. The sensitivity of this technique to changes in the optical parameters can be evaluated by the relative errors on ua and us'. These errors are typically within a few percent.

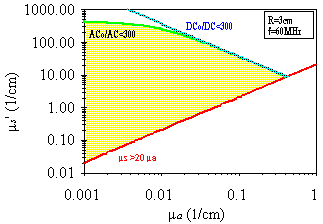
 Fig. 5. Values of ua and us' that can be measured with our instrument the frequency-domain LED technique. The conditions discussed in the text define the measurable region in the us'-ua plane, which is shown shaded. Note that the typical values of ua and us' in tissues (ua~0.01-0.1 1/cm, us'~1-100 1/cm) fall inside the measurable region.
 
 

This work has dealt with a macroscopically homogeneous strongly scattering medium in a quasi-infinite geometry. Of course, the application of this technique to in vivo spectroscopy of tissues requires some further developments. First, biological tissues are not as homogeneous as an aqueous Liposyn solution. Second, they do not provide a quasi-infinite geometry (at least for non-invasive applications). The first point has already been considered, [9 ,19] and the reasonable results obtained in vivo on the basis of homogeneous medium models are encouraging. The second point requires the use of different boundary conditions. A first approach might be that of a semi-infinite geometry with source and detector placed on the surface. Although the diffusion approximation is not valid in such a geometry, it still constitutes a reasonable starting point [9]. We are currently working on this subject.

 Several characteristics of the LED technique make it attractive from a practical standpoint:
 
 

5. ACKNOWLEDGMENTS
This work was performed at the Laboratory for Fluorescence Dynamics at the University of Illinois at Urbana- Champaign (UIUC), which is supported by the National Institutes of Health (NIH), grant RR03155 and by UIUC. This research is also supported by grant CA57032 from the NIH. The authors thank Julie Butzow for help in preparing this paper.

6. REFERENCES
  1. G. Wagnieres, C. Depeursinge, P. Monnier, M. Savary, P. Cornaz, A. Chatelain, and H. van den Bergh, "Photodetection of Early Cancer by Laser Induced Fluorescence of a Tumor-Selective Dye: Apparatus Design and Realization," Proc. SPIE - Int. Soc. Opt. Eng. (USA) 1203, 43-52 (1990). back
  2. M. S. Patterson, B. C. Wilson, J. W. Feather, D. M. Burns, and W. Pushka, "The Measurement of Dihematopotphyrin Ether Concentration in Tissue by Reflectance Spectrophotometry," Photochem. Photobiol. 46, 337-343 (1987). back
  3. M. Cope and D. T. Delpy, "System for Long-Term Measurement of Cerebral Blood and Tissue Oxygenation on Newborn Infants by Near Infrared Transillumination," Med. Biol. Eng. Comput. 26, 289-294 (1988). back
  4. B. C. Wilson and M. S. Patterson, "The Physics of Photodynamic Therapy," Phys. Med. Biol. 31, 327- 360 (1986). back
  5. S. L. Jacques and S. A. Prahl, "Modeling Optical and Thermal Distribution in Tissue During Laser Irradiation," Laser Surg. Med. 6, 494-503 (1987). back
  6. F. F. Jobsis, J. H. Keizer, J. C. LaManna, and M. Rosenthal, "Reflectance Spectrophotometry of cytochrome aa3 in vivo," J. Appl. Physiol. 43, 858-872 (1977). back
  7. P. Parsa, S. L. Jacques, and N. S. Nishioka, "Optical Properties of Rat Liver Between 350 and 2200 nm," Appl. Opt. 28, 2325-2330 (1989). back
  8. T. J. Farrel, M. S. Patterson, and B. Wilson, "A Diffusion Theory Model of Spatially Resolved, Steady-State Diffuse Reflectance for the Noninvasive Determination of Tissue Optical Properties in vivo," Med. Phys. 19, 879-888 (1992). back
  9. M. S. Patterson, B. Chance, and B. C. Wilson, "Time Resolved Reflectance and Transmittance for the Noninvasive Measurement of Tissue Optical Properties," Appl. Opt. 28, 2331-2336 (1989). back
  10. M. S. Patterson, J. D. Moulton, B. C. Wilson, K. W. Berndt, and J. R. Lakowicz, "Frequency-Domain Reflectance for the Determination of the Scattering and Absorption Properties of Tissue," Appl. Opt. 30, 4474-4476 (1991). back
  11. J. B. Fishkin, E. Gratton, M. J. van de Ven, and W. W. Mantulin, "Diffusion of Intensity Modulated Near-IR Light in Turbid Media," in Time Resolved Spectroscopy and Imaging of Tissues, B. Chance editor, Proc. SPIE 1431, 122-135 (1991). back
  12. J. B. Fishkin and E. Gratton, "Propagation of Photon-Density Waves in Strongly Scattering Media Containing an Absorbing Semi-Infinite Plane Bounded by a Straight Edge," J. Opt. Soc. Am. A 10, 127-140 (1993). back
  13. W. F. Cheong, S. A. Prahl, and A. J. Welch, "A Review of the Optical Properties of Biological Tissues," IEEE J. Quantum Electron. 26, 2166-2185 (1990). back
  14. Aldrich Chemical Company Laboratories, Milwaukee, Wisconsin (1993). back
  15. R. D. Spencer and G. Weber, "Measurement of Subnanosecond Fluorescence Lifetime with a Cross-Correlation Phase Fluorometer," Ann. N. Y. Acad. Sci. 158, 361-376 (1969). back
  16. B. A. Feddersen, D. W. Piston, and E. Gratton, "Digital Parallel Acquisition in Frequency Domain Fluorometry," Rev. Sci. Instrum. 60, 2929-2936 (1989). back
  17. G. M. Hale and M. R. Querry, "Optical Constants of Water in the 200 nm to 200 um Wavelength Region," Appl. Opt. 12, 555-563 (1973). back
  18. H. J. van Staveren, C. J. M. Moes, J. van Marle, S. A. Prahl, and M. J. C. van Gemert, "Light Scattering in Intralipid-10% in the Wavelength Range of 400-1100 nm," Appl. Opt. 30, 4507-4514 (1991). back
  19. E. M. Sevick, B. Chance, J. Leigh, S. Nioka, and M. Maris, "Quantitation of Time- and Frequency-Resolved Optical Spectra for the Determination of Tisuue Oxigenation," Anal. Biochem. 195, 330-351 (1991). back
Back to top