Returns STC files ie source estimates of induced power for different bands in the source space. The inverse method is linear based on dSPM inverse operator.
# Authors: Alexandre Gramfort <alexandre.gramfort@telecom-paristech.fr>
#
# License: BSD (3-clause)
import matplotlib.pyplot as plt
import mne
from mne import io
from mne.datasets import sample
from mne.minimum_norm import read_inverse_operator, source_band_induced_power
print(__doc__)
Set parameters
data_path = sample.data_path()
raw_fname = data_path + '/MEG/sample/sample_audvis_raw.fif'
fname_inv = data_path + '/MEG/sample/sample_audvis-meg-oct-6-meg-inv.fif'
tmin, tmax, event_id = -0.2, 0.5, 1
# Setup for reading the raw data
raw = io.read_raw_fif(raw_fname)
events = mne.find_events(raw, stim_channel='STI 014')
inverse_operator = read_inverse_operator(fname_inv)
include = []
raw.info['bads'] += ['MEG 2443', 'EEG 053'] # bads + 2 more
# picks MEG gradiometers
picks = mne.pick_types(raw.info, meg=True, eeg=False, eog=True,
stim=False, include=include, exclude='bads')
# Load condition 1
event_id = 1
events = events[:10] # take 10 events to keep the computation time low
# Use linear detrend to reduce any edge artifacts
epochs = mne.Epochs(raw, events, event_id, tmin, tmax, picks=picks,
baseline=(None, 0), reject=dict(grad=4000e-13, eog=150e-6),
preload=True, detrend=1)
# Compute a source estimate per frequency band
bands = dict(alpha=[9, 11], beta=[18, 22])
stcs = source_band_induced_power(epochs, inverse_operator, bands, n_cycles=2,
use_fft=False, n_jobs=1)
for b, stc in stcs.items():
stc.save('induced_power_%s' % b)
Out:
Opening raw data file /home/ubuntu/mne_data/MNE-sample-data/MEG/sample/sample_audvis_raw.fif...
Read a total of 3 projection items:
PCA-v1 (1 x 102) idle
PCA-v2 (1 x 102) idle
PCA-v3 (1 x 102) idle
Range : 25800 ... 192599 = 42.956 ... 320.670 secs
Ready.
Current compensation grade : 0
320 events found
Events id: [ 1 2 3 4 5 32]
Reading inverse operator decomposition from /home/ubuntu/mne_data/MNE-sample-data/MEG/sample/sample_audvis-meg-oct-6-meg-inv.fif...
Reading inverse operator info...
[done]
Reading inverse operator decomposition...
[done]
305 x 305 full covariance (kind = 1) found.
Read a total of 4 projection items:
PCA-v1 (1 x 102) active
PCA-v2 (1 x 102) active
PCA-v3 (1 x 102) active
Average EEG reference (1 x 60) active
Noise covariance matrix read.
22494 x 22494 diagonal covariance (kind = 2) found.
Source covariance matrix read.
22494 x 22494 diagonal covariance (kind = 6) found.
Orientation priors read.
22494 x 22494 diagonal covariance (kind = 5) found.
Depth priors read.
Did not find the desired covariance matrix (kind = 3)
Reading a source space...
Computing patch statistics...
Patch information added...
Distance information added...
[done]
Reading a source space...
Computing patch statistics...
Patch information added...
Distance information added...
[done]
2 source spaces read
Read a total of 4 projection items:
PCA-v1 (1 x 102) active
PCA-v2 (1 x 102) active
PCA-v3 (1 x 102) active
Average EEG reference (1 x 60) active
Source spaces transformed to the inverse solution coordinate frame
2 matching events found
Created an SSP operator (subspace dimension = 3)
3 projection items activated
Loading data for 2 events and 421 original time points ...
0 bad epochs dropped
Preparing the inverse operator for use...
Scaled noise and source covariance from nave = 1 to nave = 1
Created the regularized inverter
Created an SSP operator (subspace dimension = 3)
Created the whitener using a full noise covariance matrix (3 small eigenvalues omitted)
Computing noise-normalization factors (dSPM)...
[done]
Picked 305 channels from the data
Computing inverse...
(eigenleads need to be weighted)...
Reducing data rank to 302
Computing source power ...
[done]
[done]
Writing STC to disk...
[done]
Writing STC to disk...
[done]
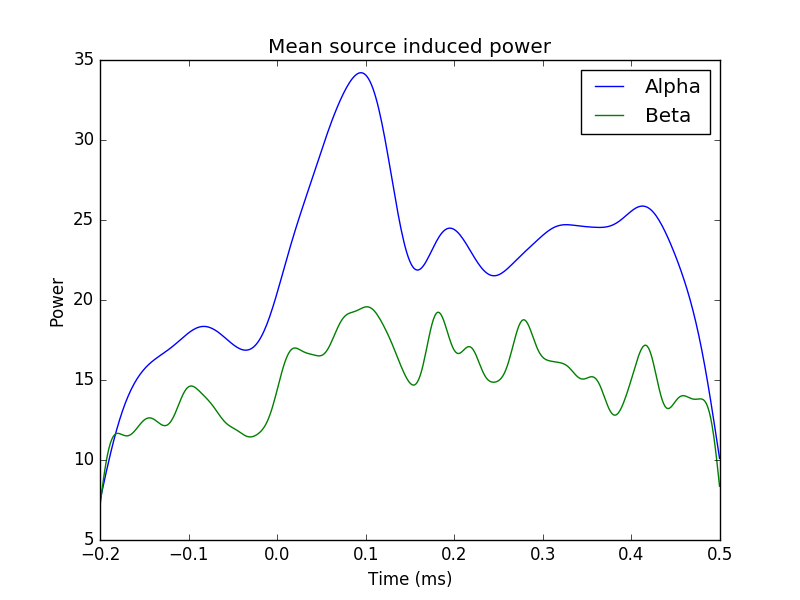
plot mean power
plt.plot(stcs['alpha'].times, stcs['alpha'].data.mean(axis=0), label='Alpha')
plt.plot(stcs['beta'].times, stcs['beta'].data.mean(axis=0), label='Beta')
plt.xlabel('Time (ms)')
plt.ylabel('Power')
plt.legend()
plt.title('Mean source induced power')
plt.show()
Total running time of the script: ( 0 minutes 7.855 seconds)