import os.path as op
import mne
from mne.datasets import sample
Source estimation method such as MNE require a noise estimations from the recordings. In this tutorial we cover the basics of noise covariance and construct a noise covariance matrix that can be used when computing the inverse solution. For more information, see Computing the noise-covariance matrix.
data_path = sample.data_path()
raw_empty_room_fname = op.join(
data_path, 'MEG', 'sample', 'ernoise_raw.fif')
raw_empty_room = mne.io.read_raw_fif(raw_empty_room_fname)
raw_fname = op.join(data_path, 'MEG', 'sample', 'sample_audvis_raw.fif')
raw = mne.io.read_raw_fif(raw_fname)
raw.set_eeg_reference()
raw.info['bads'] += ['EEG 053'] # bads + 1 more
Out:
Opening raw data file /home/ubuntu/mne_data/MNE-sample-data/MEG/sample/ernoise_raw.fif...
Isotrak not found
Read a total of 3 projection items:
PCA-v1 (1 x 102) idle
PCA-v2 (1 x 102) idle
PCA-v3 (1 x 102) idle
Range : 19800 ... 85867 = 32.966 ... 142.965 secs
Ready.
Current compensation grade : 0
Opening raw data file /home/ubuntu/mne_data/MNE-sample-data/MEG/sample/sample_audvis_raw.fif...
Read a total of 3 projection items:
PCA-v1 (1 x 102) idle
PCA-v2 (1 x 102) idle
PCA-v3 (1 x 102) idle
Range : 25800 ... 192599 = 42.956 ... 320.670 secs
Ready.
Current compensation grade : 0
Adding average EEG reference projection.
1 projection items deactivated
The definition of noise depends on the paradigm. In MEG it is quite common
to use empty room measurements for the estimation of sensor noise. However if
you are dealing with evoked responses, you might want to also consider
resting state brain activity as noise.
First we compute the noise using empty room recording. Note that you can also
use only a part of the recording with tmin and tmax arguments. That can be
useful if you use resting state as a noise baseline. Here we use the whole
empty room recording to compute the noise covariance (tmax=None is the same
as the end of the recording, see mne.compute_raw_covariance()).
noise_cov = mne.compute_raw_covariance(raw_empty_room, tmin=0, tmax=None)
Out:
Using up to 549 segments
Number of samples used : 65880
[done]
Now that you the covariance matrix in a python object you can save it to a
file with mne.write_cov(). Later you can read it back to a python
object using mne.read_cov().
You can also use the pre-stimulus baseline to estimate the noise covariance. First we have to construct the epochs. When computing the covariance, you should use baseline correction when constructing the epochs. Otherwise the covariance matrix will be inaccurate. In MNE this is done by default, but just to be sure, we define it here manually.
events = mne.find_events(raw)
epochs = mne.Epochs(raw, events, event_id=1, tmin=-0.2, tmax=0.0,
baseline=(-0.2, 0.0))
Out:
320 events found
Events id: [ 1 2 3 4 5 32]
72 matching events found
Created an SSP operator (subspace dimension = 4)
4 projection items activated
Note that this method also attenuates the resting state activity in your source estimates.
noise_cov_baseline = mne.compute_covariance(epochs)
Out:
Loading data for 72 events and 121 original time points ...
0 bad epochs dropped
Estimating covariance using EMPIRICAL
Done.
Using cross-validation to select the best estimator.
Number of samples used : 8712
[done]
log-likelihood on unseen data (descending order):
empirical: -1837.298
selecting best estimator: empirical
Try setting proj to False to see the effect. Notice that the projectors in
epochs are already applied, so proj parameter has no effect.
noise_cov.plot(raw_empty_room.info, proj=True)
noise_cov_baseline.plot(epochs.info)
Out:
Created an SSP operator (subspace dimension = 3)
The estimated covariance can be numerically unstable and tends to induce correlations between estimated source amplitudes and the number of samples available. The MNE manual therefore suggests to regularize the noise covariance matrix (see Regularization of the noise-covariance matrix), especially if only few samples are available. Unfortunately it is not easy to tell the effective number of samples, hence, to choose the appropriate regularization. In MNE-Python, regularization is done using advanced regularization methods described in [1]. For this the ‘auto’ option can be used. With this option cross-validation will be used to learn the optimal regularization:
cov = mne.compute_covariance(epochs, tmax=0., method='auto')
Out:
Loading data for 72 events and 121 original time points ...
Estimating covariance using SHRUNK
Done.
Estimating covariance using DIAGONAL_FIXED
EEG regularization : None
MAG regularization : 0.01
GRAD regularization : 0.01
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using FACTOR_ANALYSIS
... rank: 5 - loglik: -1889.922
... rank: 10 - loglik: -1852.016
... rank: 15 - loglik: -1829.413
... rank: 20 - loglik: -1816.381
... rank: 25 - loglik: -1805.784
... rank: 30 - loglik: -1797.708
... rank: 35 - loglik: -1792.948
... rank: 40 - loglik: -1791.404
... rank: 45 - loglik: -1789.788
... rank: 50 - loglik: -1788.293
... rank: 55 - loglik: -1787.154
... rank: 60 - loglik: -1786.771
... rank: 65 - loglik: -1786.254
... rank: 70 - loglik: -1786.301
... rank: 75 - loglik: -1786.192
... rank: 80 - loglik: -1786.915
... rank: 85 - loglik: -1786.300
... rank: 90 - loglik: -1786.785
... rank: 95 - loglik: -1786.508
... rank: 100 - loglik: -1786.828
... rank: 105 - loglik: -1786.391
... rank: 110 - loglik: -1786.858
... rank: 115 - loglik: -1787.574
... rank: 120 - loglik: -1787.115
early stopping parameter search.
... best model at rank = 75
Done.
Using cross-validation to select the best estimator.
EEG regularization : None
MAG regularization : 0.01
GRAD regularization : 0.01
EEG regularization : None
MAG regularization : 0.01
GRAD regularization : 0.01
EEG regularization : None
MAG regularization : 0.01
GRAD regularization : 0.01
Number of samples used : 8712
[done]
Number of samples used : 8712
[done]
Number of samples used : 8712
[done]
Number of samples used : 8712
[done]
log-likelihood on unseen data (descending order):
shrunk: -1772.255
factor_analysis: -1786.192
diagonal_fixed: -1795.956
empirical: -1837.298
selecting best estimator: shrunk
This procedure evaluates the noise covariance quantitatively by how well it
whitens the data using the
negative log-likelihood of unseen data. The final result can also be visually
inspected.
Under the assumption that the baseline does not contain a systematic signal
(time-locked to the event of interest), the whitened baseline signal should
be follow a multivariate Gaussian distribution, i.e.,
whitened baseline signals should be between -1.96 and 1.96 at a given time
sample.
Based on the same reasoning, the expected value for the global field power
(GFP) is 1 (calculation of the GFP should take into account the true degrees
of freedom, e.g. ddof=3 with 2 active SSP vectors):
evoked = epochs.average()
evoked.plot_white(cov)
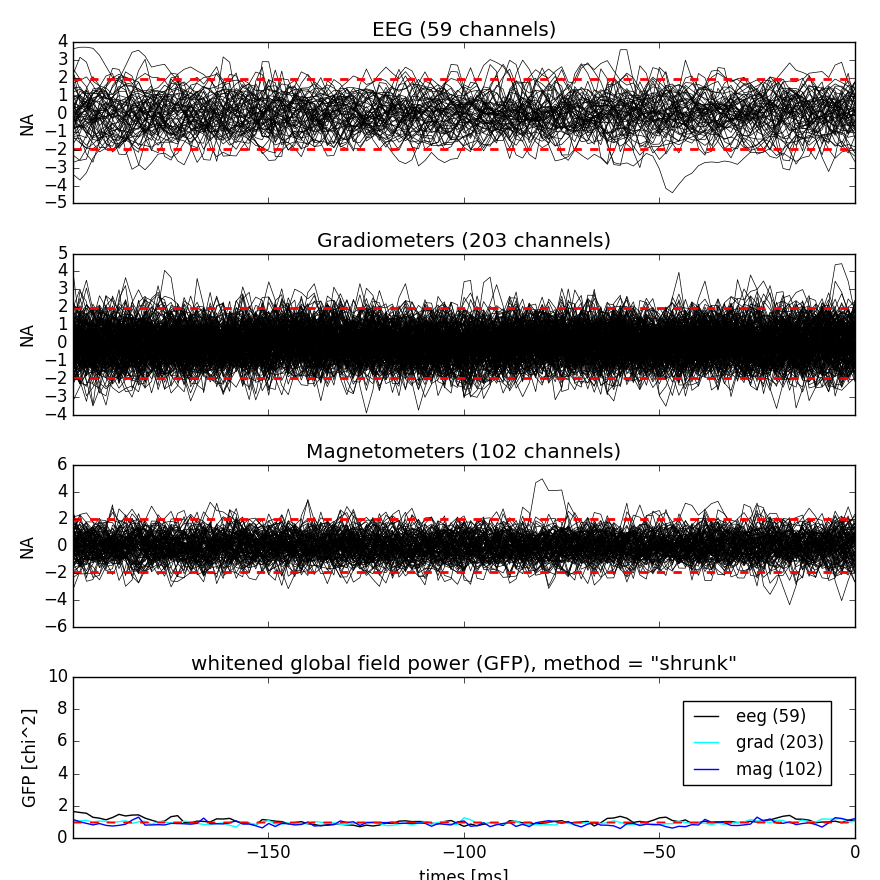
Out:
estimated rank (eeg): 59
estimated rank (grad): 203
estimated rank (mag): 102
estimated rank (mag + grad): 305
estimated rank (eeg): 59
Created an SSP operator (subspace dimension = 4)
Setting small MEG eigenvalues to zero.
Not doing PCA for MEG.
Setting small EEG eigenvalues to zero.
Not doing PCA for EEG.
This plot displays both, the whitened evoked signals for each channels and the whitened GFP. The numbers in the GFP panel represent the estimated rank of the data, which amounts to the effective degrees of freedom by which the squared sum across sensors is divided when computing the whitened GFP. The whitened GFP also helps detecting spurious late evoked components which can be the consequence of over- or under-regularization.
Note that if data have been processed using signal space separation (SSS) [2], gradiometers and magnetometers will be displayed jointly because both are reconstructed from the same SSS basis vectors with the same numerical rank. This also implies that both sensor types are not any longer statistically independent. These methods for evaluation can be used to assess model violations. Additional introductory materials can be found here.
For expert use cases or debugging the alternative estimators can also be compared:
covs = mne.compute_covariance(epochs, tmax=0., method=('empirical', 'shrunk'),
return_estimators=True)
evoked = epochs.average()
evoked.plot_white(covs)
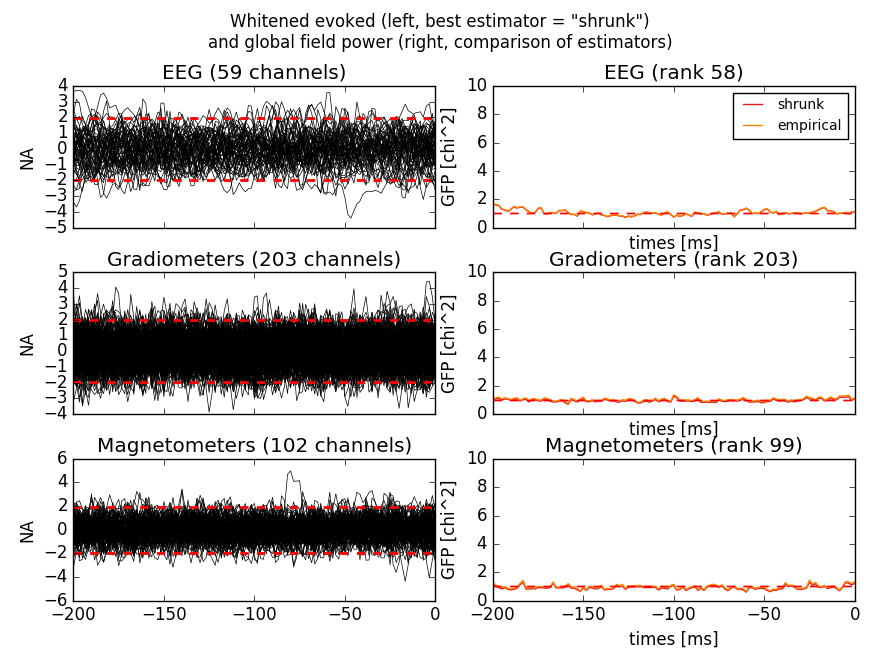
Out:
Loading data for 72 events and 121 original time points ...
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using SHRUNK
Done.
Using cross-validation to select the best estimator.
Number of samples used : 8712
[done]
Number of samples used : 8712
[done]
log-likelihood on unseen data (descending order):
shrunk: -1772.255
empirical: -1837.298
estimated rank (eeg): 59
estimated rank (grad): 203
estimated rank (mag): 102
estimated rank (mag + grad): 305
estimated rank (eeg): 59
estimated rank (eeg): 58
estimated rank (grad): 203
estimated rank (mag): 99
estimated rank (mag + grad): 302
estimated rank (eeg): 58
Created an SSP operator (subspace dimension = 4)
Setting small MEG eigenvalues to zero.
Not doing PCA for MEG.
Setting small EEG eigenvalues to zero.
Not doing PCA for EEG.
Created an SSP operator (subspace dimension = 4)
Setting small MEG eigenvalues to zero.
Not doing PCA for MEG.
Setting small EEG eigenvalues to zero.
Not doing PCA for EEG.
This will plot the whitened evoked for the optimal estimator and display the GFPs for all estimators as separate lines in the related panel.
| [1] | Engemann D. and Gramfort A. (2015) Automated model selection in covariance estimation and spatial whitening of MEG and EEG signals, vol. 108, 328-342, NeuroImage. |
| [2] | Taulu, S., Simola, J., Kajola, M., 2005. Applications of the signal space separation method. IEEE Trans. Signal Proc. 53, 3359-3372. |
Total running time of the script: ( 4 minutes 12.715 seconds)